Affine manifold
In differential geometry, an affine manifold is a manifold equipped with a flat, torsion-free connection.
Equivalently, it is a manifold that is (if connected) covered by an open subset of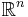 
, with monodromy acting by affine transformations. This equivalence is an easy corollary of Cartan-Ambrose-Hicks theorem.
Equivalently, it is a manifold equipped with an atlas—called the affine structure—with all transition functions between charts affine (that is, have constant jacobian matrix); two atlases are equivalent if the manifold admits an atlas subjugated to both, with transitions from both atlases to a smaller atlas being affine. A manifold having a distinguished affine structure is called an affine manifold and the charts which are affinely related to those of the affine structure are called affine charts. In each affine coordinate domain the coordinate vector fields form a parallelization of that domain, so there is an associated connection on each domain. These locally defined connections are the same on overlapping parts, so there is a unique connection associated with an affine structure.
Contents |
Formal definition
An affine manifold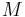 
is a real manifold with charts 
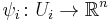such that 
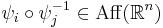for all 
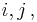where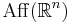 
denotes the Lie group of affine transformations.
An affine manifold is called complete if its universal covering is isomorphic to .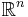
A fundamental group of a compact complete flat affine manifold is called an affine crystallographic group. Classification of affine crystallographic groups is a difficult problem, far from being solved. The Riemannian crystallographic groups (also known as Bieberbach groups) were classified by L. Bieberbach, answering a question posed by Hilbert. In his work on Hilbert's 18-th problem, Bieberbach proved that any Riemannian crystallographic group contains an abelian subgroup of finite index.
Important longstanding conjectures
Geometry of affine manifolds is essentially a network of longstanding conjectures; most of them proven in low dimension and some other special cases.
The most important of them are
- Markus conjecture (1961) stating that a compact affine manifold is complete if and only if it has constant volume.[1] Known in dimension 3.
- Auslander conjecture (1964)[2][3] stating that any affine crystallographic group contains a polycyclic subgroup of finite index. Known in dimensions up to 6,[4] and when the holonomy of the flat connection preserves a Lorentz metric.[5] Since every virtually polycyclic crystallographic group preserves a volume form, Auslander conjecture implies the "only if" part of the Markus conjecture.[6]
- Chern conjecture (1955) The Euler class of an affine manifold vanishes.[7]
Notes
- ^ Hirsch M. and Thurston W., Foliated bundles, invariant measures, and flat manifolds, Ann. Math. (2) 101, (1975) 369-390.
- ^ Auslander L., The structure of locally complete affine manifolds, Topology 3 (1964), 131-139.
- ^ Fried D. and Goldman W., Three dimensional affine crystallographic groups, Adv. Math. 47 (1983), 1-49.
- ^ H. Abels, G. A. Margulis and G. A. Soifer, On the Zariski closure of the linear part of a properly discontinuous group of affine transformations, J. Differential Geom., 60 (2002), 315344.
- ^ William M. Goldman and Yoshinobu Kamishima, The fundamental group of a compact flat Lorentz space form is virtually polycyclic, J. Differential Geom. Volume 19, Number 1 (1984)
- ^ Herbert Abels, Properly Discontinuous Groups of Affine Transformations: A Survey, Geom. Dedicata, 87,. 309–333 (2001)
- ^ Konstant B., Sullivan D., The Euler characteristic of an affine space form is zero, Bull. Amer. Math. Soc. 81 (1975), no. 5, 937-938.